汉诺塔永远只有三步:
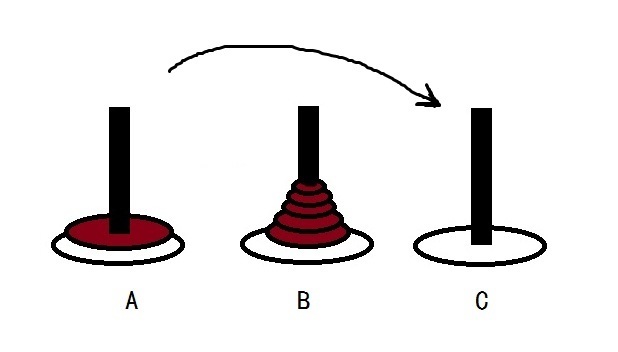
思路
此问题可以简化为三个步骤
要想把A柱盘子全部移到C柱
- 把n-1(最后一个盘上面的所有盘子)盘移动到B柱
- 把第n个盘子(最后一个盘子)移到C柱
- 把n-1那一堆盘子移到C柱 那么问题来了,如何把那n-1个盘子移到B柱呢,当然是继续分解为n-2啦,也即调用自身函数进行递归,递归的边界就是n = 1喽。
python代码
1
2
3
4
5
6
7
8
9
10
11
#-*- using utf-8 -*-
def move(n, a, b, c):
if n == 1:
print(a,'-->',c)
else:
move(n - 1, a, c, b)
move(1, a, b, c)
move(n - 1, b, a, c)
move(3, 'A', 'B', 'C')
C代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <cstdio>
using namespace std;
void move(int n, char a, char b, char c)
{
if (n == 1)
{
printf("%c --> %c\n",a, c);
}
else
{
move(n - 1, a, c, b);
move(1, a, b, c);
move(n - 1, b, a, c);
}
}
int main()
{
int n = 3;
char a = 'A', b = 'B', c = 'C';
move(n, a, b, c);
return 0;
}